
푸앵카레의 추측 - 100년만에 풀린 난제
- 319호
- 기사입력 2015.03.13
- 취재 김나현 기자
- 편집 김혜린 기자
- 조회수 15756

눈앞에 아래의 물건들이 놓여 있다고 생각해보자. 저것들이 무엇이냐고 묻는다면, 곧 농구공, 스푼, 도넛이라는 세 개의 이름들이 불린다. 일상생활에서는 당연하게도 저 세 개가 모두 다른 물체이다. 하지만 위상기하학(Topology)의 관점에서 저 물체들은 두 개의 다양체로 구별된다. 숟가락과 농구공은 구(sphere)로, 도넛은 원환면(圓環面 - torus)로 바꿀 수 있다. 익숙치 않은 단어인 원환면이란, 삼차원 상에서 직선축을 중심으로 원을 한 바퀴 회전시킨 것이다. 이 때 원은 직선축과 떨어져 있어 회전하고 나면 우리가 흔히 아는 도넛모양이 만들어지게 된다.

아하, 원환면은 결국 도넛모양의 물체인 것이다. 다만 의문이 가시지 않는 것은 숟가락이 구로 바뀐다는 것이다. 더 간단명료하게 농구공과 도넛을 비교해보자.

농구공과 도넛에 줄을 걸어보는 것이다. 시작점과 끝점이 만나야 한다. 농구공에 둥글게 줄을 거는 모양은 하나밖에 없지만 도넛은 여러 방향으로 걸어볼 수 있을 것이다. 줄의 시작점과 끝점이 같아지게 줄을 걸었다면 이제 한쪽 줄을 당겨보자. 이 때 줄이 물체의 표면을 떠서는 안된다. 농구공의 경우는 줄이 막힘없이 올라와 결국은 하나의 점처럼 모인다. 도넛의 경우, 수평으로 줄을 걸었다면 당기는 중간에 구멍 위로 줄이 떠버릴 것이고, 구멍 안으로 걸었다면 도넛두께에 줄이 걸리게 된다. 한 점으로 모이지 않는다는 것이다.
농구공은 줄을 당기면 마치 한 점처럼 모을 수 있으나, 도넛은 어떤 방향으로 걸어도 줄을 당겼을 때 하나의 점으로 모일 수 없다. 숟가락은 어떨까? 숟가락 또한 농구공과 마찬가지이다. 줄을 당겨보았을 때 어렵지 않게 하나의 점으로 모이는 것을 직관적으로 알 수 있기 때문이다. 이런 경우 위상기하학의 관점에서는 숟가락도 농구공과 같은 하나의 구(sphere)라고 보는 것이다.
그렇다면 물체에 밧줄을 걸었을 때, 당겨서 하나의 점으로 만들 수 있다면 우리는 그것이 ‘구(sphere)’인 것을 수학적으로 ‘증명’할 수 있는가? 직관적인 생각을 떠나 수학적인 증명을 묻는 ‘푸앵카레의 추측(Poincaré conjecture)’은 여기서부터 출발한다.

앙리 푸앵카레는 프랑스에서 태어난 수학자요 물리학자였다. ‘지(知)의 거인’이라고 불릴 정도로 생물학, 철학 등 다양한 분야에서 두각을 나타냈던 그는 의외로, 논리를 속박이라고 생각했다. 직감적인 착상을 더 중요하게 여겼던 그는 미분기하학(Differential Geometry)의 세계에서 위상기하학(Topology)을 더 매력적으로 느꼈던 것이다. 위상기하학의 세계에서 원과 세모는 같다. 늘이고 줄여서 서로 겹쳐 맞출 수 있는 평면도형은 그 평면 위에서 동위(同位)인 도형이기 때문이다. 평면뿐만 아니라 공간에서도 마찬가지다. 따라서 숟가락은 길이를 줄이고 마치 공기를 넣듯 부풀리면 끝내 농구공과 같은 모양을 가지게 되니, 숟가락과 농구공은 동위(同位)라고 할 수 있는 것이다.
이렇게 위상기하학의 관점에서 모든 물체들을 간단히 구(sphere)나 도넛같이 구멍을 가진 원환면(torus) 또는 이들의 복합체로 생각해 볼 수 있게 된다. 이런 생각이 가장 획기적으로 쓰이는 곳은 지구나 우주의 형태를 추측하는 데 있다. 푸앵카레는 19세기 말, 20세기 초의 사람으로 아직 인간이 우주로 나가 지구의 모습을 직접 볼 수 없었던 시대에 살았다. 이미 16세기 즈음에 대항해시대를 맞아 세계 일주도 성공하면서 지구가 둥글다는 것을 암묵적으로 체험했던 역사가 있었다. 하지만 푸앵카레는 지구가 도넛모양이라도 세계일주가 가능하다는 점을 짚었다. 이번에는 항구에 밧줄을 단단히 묶고 한쪽 끝을 배에 고정시켜 세계일주를 시켜보자. 항구로 다시 돌아온 배의 밧줄한쪽을 잡고 계속 당겨서 모두 회수가 가능하다면 지구는 둥글다고 확신할 수 있지 않을까?
우주의 모양은 지구와 달리 훨씬 더 거대한 영역이자 우리가 경험적으로 확인할 수 없다. 푸앵카레의 추측은 지구의 모양을 논할 때도 획기적이었지만, 직접 우주 밖에서 모양을 볼 수 없는 문제에 대해서는 탁월한 힘을 발휘한다. 로켓에 줄을 매달고 우주를 한바퀴 돌고 지구에 착륙한다. 지구에서 로켓에 매단 줄을 모두 회수할 수 있다면 우리는 우주가 구(sphere)를 이룬다고 말할 수 있을까? 많은 학자들이 푸앵카레의 추측을 두고 증명하려 고군분투했다.

푸앵카레의 추측은 1904년 그가 50살이 되던 해에 세상에 나왔다.
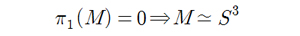

생소한 단어들로 이루어진 명제이지만 익숙한 단어로 바꿔볼 수 있다. 단일연결이란 말하자면 시작과 끝점이 같은 선(폐곡선)이 한 점으로 수축될 수 있다는 것을 의미한다. 3차원의 닫힌 다양체는 우리가 위에서 본 숟가락이나 농구공 따위로 볼 수 있으며 3차원 구는 우리가 관용적으로 이해하는 구(sphere)이다. 단순히 밧줄과 로켓으로 직관적인 생각을 했던 것과는 달리 수학적인 식으로 ‘증명’을 하기까지는 매우 어려웠다. 수많은 수학자들이 이 추측을 풀기위해 평생을 바치고 죽었기 때문이다. 그러나 1904년 푸앵카레의 추측이 세상에 나온 이후로 증명은 차원단계로 차근차근히 증명되었다. 5차원 이상의 다양체에 해당하는 증명은 스티븐 스메일(Stephen Smail) 박사가 증명했으며, 4차원 증명은 마이클 프리드먼(Michael H. freedman)박사가 해내어 둘 모두 영예의 필즈상을 수상하였다.

20세기의 막바지 즈음, 3차원에서의 증명은 여전히 미궁 속에 있었다. 다만 3차원의 약간의 실마리를 제기한 것은 윌리엄 서스턴(Willian Paul Thurston)이다. 우주의 형태를 만드는 원료가 총 8개만 존재한다는 것이다. 이것을 ‘기하화 추측’이라고 부른다. 그에 따르면 8가지 원료에 해당하는 모형 중 오직 하나만 구의 모양을 가지고 있으며 나머지는 도넛처럼 구멍을 가지고 있다. 그렇다면 가능한 우주의 모든 모양 중에서도 쏜 밧줄을 모두 회수할 수 있는 것은 구(sphere)의 형태를 가진 우주뿐인 것이다. 기하화 추측이 증명이 된다면 푸앵카레의 추측은 큰 토대를 마련한 셈이었다. 그리고 서스턴 박사는 그것을 증명해냈다.
그리고 마침내 가장 원초적인 3차원세계의 푸앵카레의 추측을 증명해낸 것은 러시아의 수학자 ‘그레고리 페렐만(Grigory Perelman)'이었다. 밀레니엄이 도래한지 얼마 되지 않아 일어난 수학계의 대사건이었다. 3년간의 증명분석 끝에 오류가 없음을 판명했으며, 페렐만은 필즈상과 밀레니엄 상의 수상자로 선정되었다. 하지만 그는 끝끝내 수상거부의 의사를 밝히며 시상식에 나타나지 않았다. 가난한 수학자가 난제를 푼 것도 모자라 100만 불의 상금과 명예를 거부한 것은 전 세계에 대서특필되었다. 하지만 수많은 언론의 접촉시도에도 불구하고 그는 자신의 집에서 나오지 않았다. 다른 사람들은 생각조차 못할 정도로 오로지 수학문제에 투자했다. 그 시간들이 페렐만에게 낯선 관심과 원치 않은 노출이 되어 돌아왔다고 생각하는 것일까? 얼굴을 보이지 않은 채 사무적이고 회의적인 인터뷰를 했다고 전해진다. 아직도 그가 현재 무엇을 하고 있는지는 아무것도 모른다. 하지만 그가 100년 간 풀리지 않았던 문제를 푼 대단한 사람이라는 것은 명백한 사실이다.
| No. | 제목 | 등록일 | 조회 |
|---|---|---|---|
| 10 | 329호 자본주의 거품경제의 시초 튤립투기(Tulip Mania) | 2015-08-13 | 13525 |
| 9 | 327호 허가받은 약탈자, 사략선 | 2015-07-13 | 12857 |
| 8 | 325호 불로장생의 길을 여는 열쇠 텔로미어 | 2015-06-13 | 11884 |
| 7 | 323호 해장 - 건강하게 술 먹기 | 2015-05-12 | 12016 |
| 6 | 321호 신께서 허락한 음식, 할랄(Halal Food) | 2015-04-13 | 13561 |
| 5 | 319호 푸앵카레의 추측 - 100년만에 풀린 난제 | 2015-03-13 | 15756 |
| 4 | 317호 클레이 수학 연구소 - 세계 7대 난제의 탄생 | 2015-02-11 | 15047 |
| 3 | 315호 자유로운 입국을 위한 허가증, VISA | 2015-01-13 | 12108 |
| 2 | 200호 단비의 1년! | 2010-03-18 | 4554 |
| 1 | 100호 내 몸안에 또 다른 누군가가 있다면? - Chimera, 그리고 Chimera Placity | 2006-01-14 | 7285 |

